Introduction
The dual simplex algorithm is one of the best methods for solving linear programming problems. To solve linear models, CPLEX or GAMS software has been implemented. But to solve linear programming models with these softwares, they must be installed on the client and for large models, a valid license must be available. In order to make solving linear programming models simple, the optimization city group has designed and developed an online solver for solving linear programming problems. In the following, we will review how to use this online solver.
Instruction of using online solver of linear program with Dual Simplex Method
The GUI of the online solver of the Dual Simplex method is as follows.
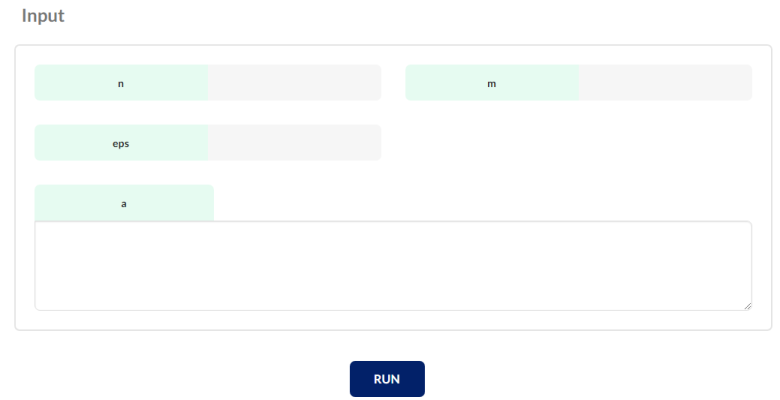
Problem input
To find the optimal solution of the linear programming problem using the dual simplex method, the required inputs are as follows:
n: number of decision variables
m: number of constraints
esp: maximum acceptable error in calculations
a: This matrix has m+1 rows and n+1 columns. a[i,j] for i=1,…,m and j=1,…,n for coefficients of constraints, a[0,j] for j=1,…,n corresponding to coefficients of variables in the objective function, and a[i,0] stores the values on the right side of the constraint.
Note: the components of matrix a can be continuous numbers.
Note: the desired model should be in standard form of dual problem (each limit is a basic variable).
Note: The coefficient values of the variables in the objective function are negative for maximization.
Example: To teach how to use this solver, we use the following example. A linear programming model with seven variables and three constraints is defined as follows.
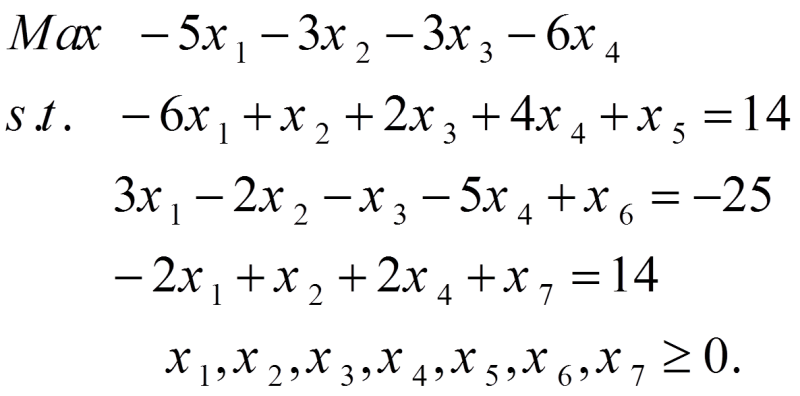
Solution: The input information for the given model is as follows.
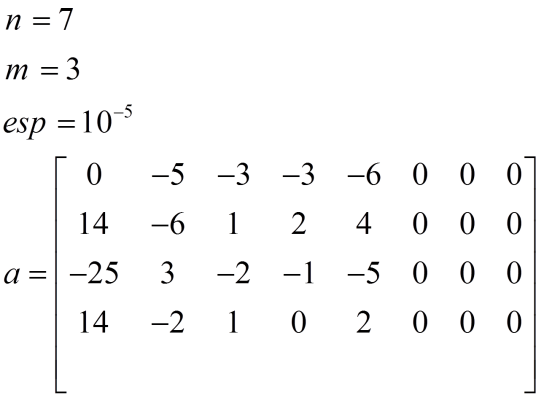
Entering information in the online solver for the linear program with dual simplex method is as follows.

After entering the data, we click on the RUN button.

The result of running the algorithm is as follows.

In the output, the phrase “Optimal solution found” means that the model has a limited optimal solution.
In the output, it reports only the values of the basic variables and the rest of the variables are equal to zero. In this example, the optimal value of the variables are:

In the last part of the output, the value of the optimal objective function is reported, which is equal to -36 in this example.
