Introduction

In graph theory, a Hamiltonian path is a path in a graph that visits each vertex exactly once. A Hamiltonian circuit (or a Hamiltonian cycle) is a circuit in a graph that visits every vertex exactly once and also returns to the starting vertex. In this graph, unlike the Eulerian graph, we do not need to go through all the edges.

There is no specific software to find the Hamiltonian cycle, and to find this circuit, the existing algorithms must be coded in one of the programming languages. The Optimization City group has developed an online solver for the problem of finding the Hamiltonian path. Below is a guide for using this online solver.

Instruction of using online solver of the Hamiltonian cycle

The GUI of the online solver of this problem is as follows:

Problem input

To find the optimal solution to the problem of finding the Hamiltonian cycle, the required inputs are as follows:

n: the number of desired graph nodes.

m: the number of edges of the desired graph.

nodei: is a vector with m+1 components, where the i-th component represents the initial node of the i-th edge.

nodej: is a vector with m+1 components, where the i-th component represents the terminal node of the i-th edge.

Example: Consider the graph below.

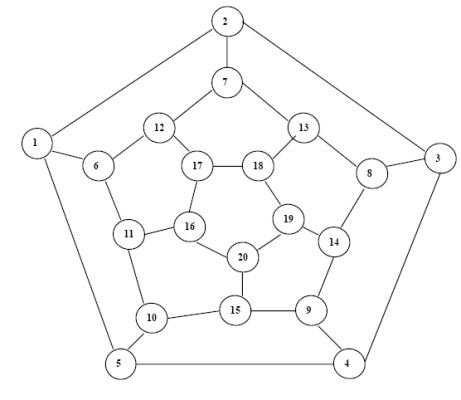
Determine the Hamiltonian path of the above graph.

Solution:

Entering information in the online solver of the Hamiltonian circuit is as follows

After entering the data, we click on the RUN button.

The result of running the algorithm is as follows.

In the output part, the nodes in the Hamiltonian path is reported.