Introduction

The k shortest paths problem is one of the most important problems in the field of operations research. In this problem, we seek to find the k shortest paths in a weighted network between the origin and the destination, where k is an integer. For example, consider the following network. For more information, you can refer to lesson 7 of Optimization City group.

Instructions of using online solver of the k shortest paths problem

The GUI of the online solver of the k shortest paths problem is as follows.

Input data

To find the k shortest paths, the required inputs are as follows:

n: the number of input network nodes

m: the number of arcs of the input network

source: source node

sink: destination node

k: the number of the shortest path from the source node to the sink node

pathnodes: A vector has two components. The first component or pathnodes[0] determines the maximum number of nodes in the shortest path despite repetition in nodes, which is an integer. The second component or pathnodes[1] determines the maximum number of the shortest path from the source to the sink destination.

nodei: a vector that specifies the initial node of the arcs and its size is for m+1.

nodej: a vector that specifies the end node of the arcs and its size is for m+1.

weight: A vector that specifies the weight or cost of bows and its size is equal to m+1.

Note 1: This solver has the possibility of using negative weights for arcs.

Note 2: The weights of the arcs must be Integer.

Note 3: The first component of the vectors nodei, nodej, and weight should be considered as zero.

Example

We use the following example to teach how to use this solver. We are looking to find the 3 shortest paths in the following network from node 5 to all nodes that are allowed to repeat nodes in the path (the maximum number of nodes allowed in this case is equal to 20). Also, we determine at most 6 shortest paths from node 5 to node 4.

Solution

The input information for the given network is as follows.

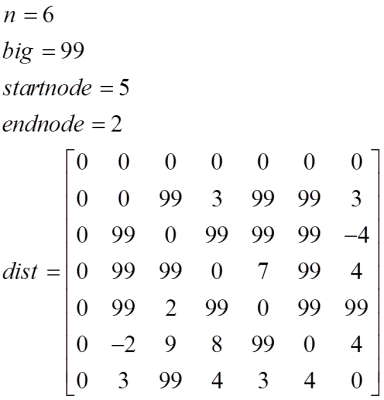
Entering information in the online solver for the k shortest paths is as follows.

After entering the data, we click on the RUN button.

The result of running the algorithm is as follows.

In the first part of the output, the 3 shortest paths from the origin node or 5 to all nodes are given. For example, the first shortest path from node 5 to node 1 equals 4; the second shortest route 9; And the third shortest path is equal to 10.

In the second part, the 6 shortest routes from node 5 to node 4 are given. In case of problem, it has been said that maximum 6 shortest routes should be stated. In some cases, when the number of all routes is less than this number, it reports the number of six routes.