Introduction

The basic assumption of many optimization models in operations research is that the variables are continuous. But in many real problems, decision variables are discrete. These problems are called integer programming models. If all decision variables are integers, the resulting model is called all integer programming model. If all the variables are zero or one (doing or not doing), it is called zero-one integer programming model. If some of the variables are integers and the rest are continuous, that model is called mixed integer programming model.

To solve these problems, there are limited softwares that need to be installed and know the programming language of those softwares. In order to make it easy to solve mixed integer programming models, the Optimization City group has designed and developed an online solver. In the following, we will review how to use this online solver.

Instruction of using online solver of mixed integer programming

The GUI of the online solver of the mixed integer programming is as follows.

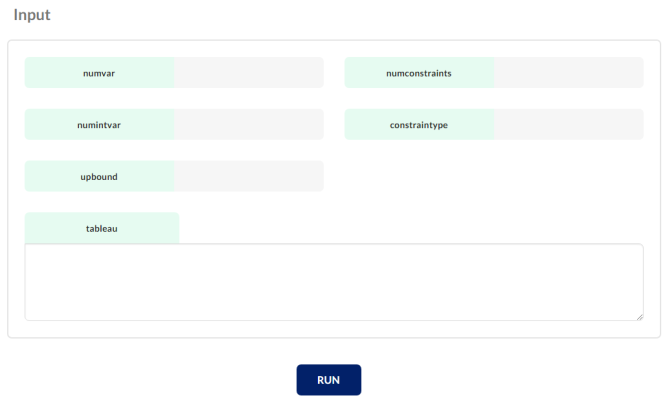
Problem input

To find the optimal solution of the mixed integer programming problem, the required inputs are as follows:

numvar: the number of all decision variables (including continuous and integer).

numconstraints: number of constraints

numintvar: number of integer decision variables

constrainttype: this vector has numconstraints+2 components. If the value is zero, it means that the constraint is the equality. If the value is -1, it means that the constraint is less-than and equality. If the value is +1, it means that the constraint is greater-than and equality.

upbound: A vector with numvar+1 component that determines the upper bound value of the variables. The first component of this vector is zero. First, the upper bound of integer variables is entered. The upper bound of continuous variables is equal to zero.

tableau: This matrix is numconstraints+3 rows and numvar+2 columns. We put zero in the first row and the numconstraints+3 row. We put zero in the first column. In the second row, we put the coefficients of the decision variables in the objective function. In the second column, we enter the values on the right hand side of the constraints. From the third row to the numconstraints+2 row, we put the coefficients of the decision variables in the constraints.

Note: In the upbound vector, integer variables are entered first and then continuous variables.

Note: Due to the comprehensiveness of this solver, this solver can be used to solve zero – one integer programming and all integer programming.

Note: The problem should be defined as minimization.

Example: To teach how to use this online solver, we use the following example. A mixed integer programming model with three integer variables, three continuous variables and six constraints is defined as follows.

Solution: The input information for the given model is as follows.

Entering information in the online solver for the mixed integer programming is as follows.

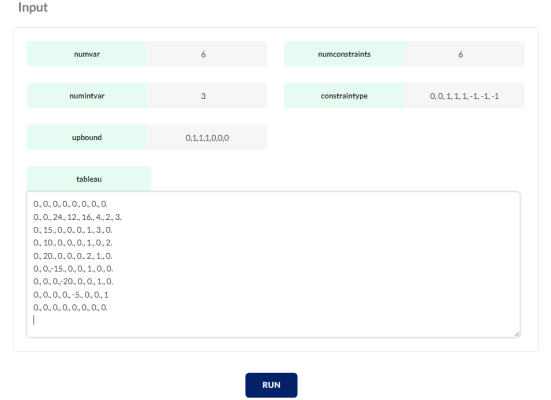
After entering the data, we click on the RUN button.

The result of running the algorithm is as follows.

In the output, the phrase “Optimal solution found” means that the model has an optimal solution.

Following the term “Solution vector”, the optimal values of decision variables are reported, which in this example we have:

In the last part of the output, the value of the optimal objective function is reported, which in this example is equal to 79.33.