Introduction

The one pair shortest path problem is one of the most important issues in the field of operations research. In this problem, we are looking for the shortest path in a weighted graph for a one pair origin-destinaiton (O-D). In Lesson 7 of Optimization City website, the shortest path algorithm is teaching with numerous examples.

Instructions of using online solver one pair shortest path problem

The GUI of the online solver of the one-pair shortest path problem is as follows:

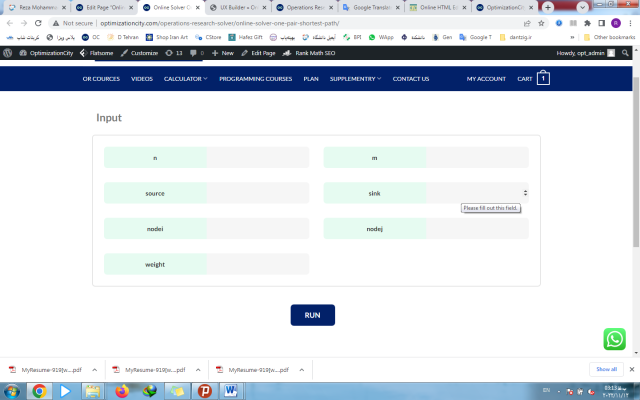
online solver of the one-pair shortest path problem optimization city

Input data

To solver the one-pair shortest path, the required inputs are:

n: the number of nodes of the input weighted graph.

m: the number of edges of the input weighted graph.

source: the source node of the input graph.

sink: The destination node is the input graph.

nodei: is a vector with m+1 components and the i-th component represents the initial node of the i-th input edges.

nodej: is a vector with m+1 components and the i-th component represents the terminal node of the i-th input edges.

weight: is a vector with m+1 components and the i-th component shows the weight of the i-th input edges.

Note: The weight of the edges must be non-negative.

Example

Find the one-pair shortest path for the following network. Node 5 is the source and node 4 is the destination.

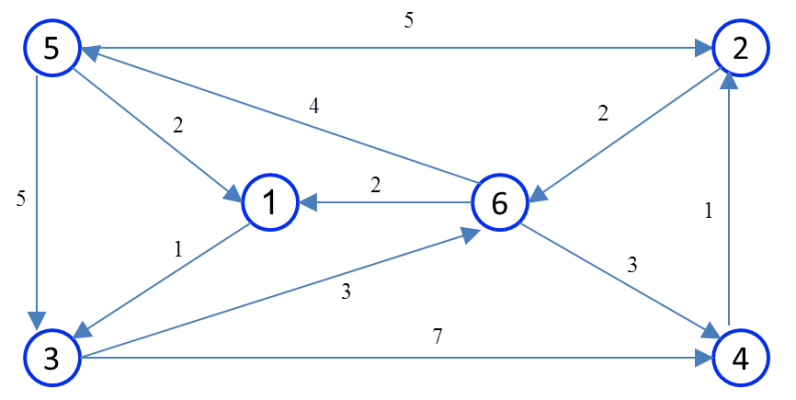
Solution:

The input data for a given network is as follows.Online Solver One Pair Shortest Path

After entering the data in the online solver, the one-pair shortest path for origin 5 to destination 4 is obtained as follows.

After entering the data, we click on the RUN button.Online Solver One Pair Shortest Path

The result of running the algorithm is as follows.

In the output part of the algorithm, the shortest route from node 5 to node 4 is that we go from 5 to 1 to 3 to 6 and finally reach destination 4. The length of the shortest path is equal to 9.