Introduction

Unlike linear programming, there is no specific algorithm for solving non-linear problems. But if nonlinear programming problems have special conditions, efficient algorithms can be used to solve them, which makes it possible to find the global optimal solution in an acceptable time. Quadratic programming is one of those non-linear programming problems that, if certain conditions exist, the global optimal solution can be solved using an algorithm based on the rule of complementary slackness and the primal simplex algorithm. In lesson 15, this algorithm is described, and those interested can refer to that lesson.

Instruction of using online solver of Quadratic programming

The GUI of the online solver of the Quadratic Programming is as follows.

Problem input

To find the optimal solution of the quadratic programming problem, the required inputs are as follows:

n: number of decision variables (continuous and non-negative)

m: number of constraints of the problem

itmax: the maximum number of iterations to improve the algorithm

a: matrix of coefficients of restrictions

b: The vector of values on the right side of the constraints

c: matrix of coefficients of quadratic variables in the objective function

d: vector of coefficients of first-order variables in the objective function

Note: Constraints must be defined as less than or equal. If the model is in the form of equality, it is possible to convert the equality constraint into two less than or equal and greater than or equal constraints and converting the greater than or equal constraint into less than or equal constraint.

Note: The model should be in minimization form.

Note: To find the optimal solution, the objective function must be convex. To show the proof of the convexity of the objective function, refer to lesson 15 of the Optimization City group.

Example: To teach how to use this online solver, we use the following example. A quadratic programming model with three variables and two constraints is defined as follows.

Solution: The input information for the given model is as follows.

Entering information in the online solver for the Quadratic programming is as follows.

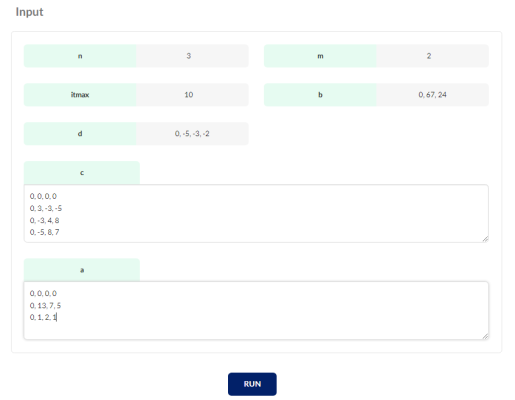
After entering the data, we click on the RUN button.

The result of running the algorithm is as follows.

In the output, the phrase “Optimal solution found” means that the model has a limited optimal solution.

In this example, the optimal value of the variables are:

In the last part of the output, the value of the optimal objective function is reported, which in this example is equal to -4.63.